문제에 뭔가 열심히 적혀있는데 결국엔 두 원이 만나는 점의 개수를 구하면 된다.
두 원의 중심이 같으면 반지름에 따라 모든 점에서 만나거나 만나는 점이 없다.
중심이 다르면 만나지 않거나, 한 점에서 접하거나, 두 점에서 만나게 된다.
이 개념만 알고 코딩하면 되는데 그게 마음처럼 쉽게 안된다. 그래서 아마 이 글을 보고 있을 것이다.
하나씩 짚어보자.
두 원의 중심이 같으면 반지름이 같은지 확인하여 반지름이 같으면 -1 출력, 다르면 0을 출력해주면 된다.
문제는 중심이 다를 때이다.
중심이 다를 때 만나지 않는 경우는 두 가지이다.
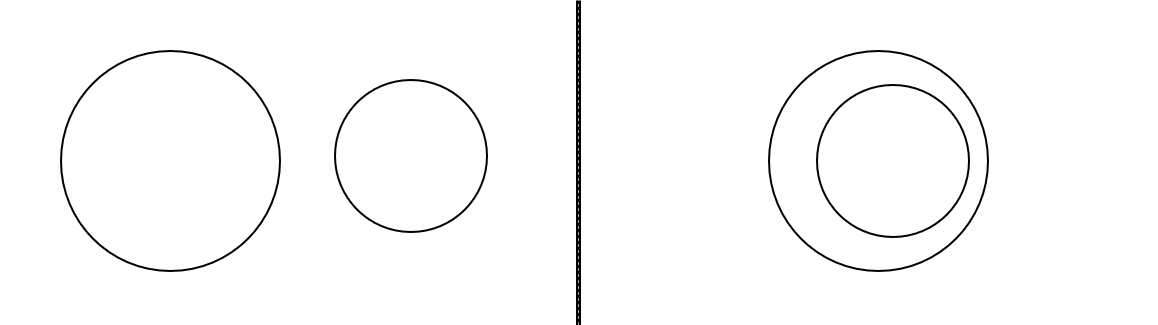
두 원이 아주 떨어져 있거나, 한 원 안에 다른 원이 들어가 있는 경우인데 나같은 경우 아주 떨어진 경우만 생각했다가 두번의 WA를 받았다.
이 두 상황을 판단하는 방법은
- 두 원이 아주 떨어져 있는 경우 : 두 원의 반지름의 합 < 두 중심 사이의 거리
- 한 원 안에 다른 원이 있는 경우 : 두 원의 반지름의 차 > 두 중심 사이의 거리
이다.
마찬가지로 두 원이 한 점에서 만나는 경우는
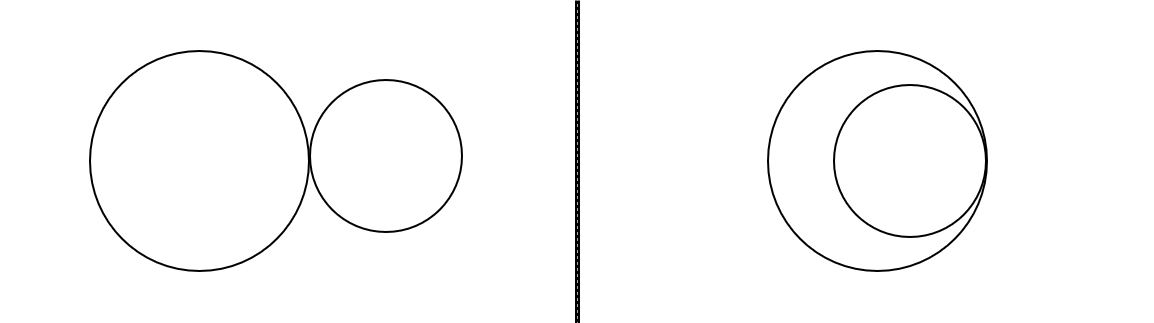
그림과 같이 두 가지 경우가 나온다.
- 두 원이 떨어져 있는 경우 : 두 원의 반지름의 합 == 두 중심 사이의 거리
- 한 원 안에 다른 원이 있는 경우 : 두 원의 반지름의 차 == 두 중심 사이의 거리
마지막으로 두 원이 두 점에서 만나는 경우는

위와 같이 두 가지 경우인 것 같아 보여서 아래와 같이
- 두 원이 떨어져 있는 경우 : 두 원의 반지름의 합 > 두 중심 사이의 거리
- 한 원 안에 다른 원이 있는 경우 : 두 원의 반지름의 차 < 두 중심 사이의 거리
나누어 생각하면 망한다. 사실 위에 두 경우는 같은 경우이므로, 두 점에서 만날 때는 위에 두 조건을 동시에 만족해야한다.
결론적으로 중심이 다를 때 두 원의 중심 사이의 거리를 \(d\), 두 원의 반지름을 \(r_1\), \(r_2\)라고 하면,
- 교점 X : \( r_1 + r_2 < d\) or \( |r_1 - r_2| > d\)
- 교점 1 : \(r_1 + r_2 = d\) or \(r_1 - r_2 = d\)
- 교점 2 : \(|r_1 - r_2| < d < r_1 + r_2\)
이렇게 정리할 수 있고, 코딩만 하면 끝난다.
#include <bits/stdc++.h>
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int T;
cin >> T;
int first_x, first_y, first_r, second_x, second_y, second_r;
int d, r;
while (T--) {
cin >> first_x >> first_y >> first_r >> second_x >> second_y >> second_r;
// d : (두 점 사이의 거리) ^ 2
d = (first_x - second_x) * (first_x - second_x) + (first_y - second_y) * (first_y - second_y);
// 중심이 같은 경우
if (d == 0) {
if (first_r == second_r) {
cout << -1 << '\n';
}
else{
cout << 0 << '\n';
}
}
// 중심이 다를 때
else {
// 미리 구해놓은 d가 거리의 제곱이므로 양변을 제곱해준다.
// r1 + r2 < d || |r1 - r2| > d
if ((first_r + second_r) * (first_r + second_r) < d || d < (first_r - second_r) * (first_r - second_r) ) {
cout << 0 << '\n';
}
// r1 + r2 == d || |r1 - r2| == d
else if ((first_r + second_r) * (first_r + second_r) == d || (first_r - second_r) * (first_r - second_r) == d) {
cout << 1 << '\n';
}
// |r1 - r2| < d < r1 + r2
else if ((first_r - second_r) * (first_r - second_r) < d && d < (first_r + second_r) * (first_r + second_r) ){
cout << 2 << '\n';
}
}
}
return 0;
}
'BOJ_단계별로 풀어보기(9단계~) > [8단계] 기본 수학2' 카테고리의 다른 글
| [백준 3053] 택시 기하학 (0) | 2021.07.29 |
|---|---|
| [백준 4153] 직각삼각형 (0) | 2021.07.28 |
| [백준 3009] 네번째 점 (0) | 2021.07.28 |
| [백준 1085] 직사각형에서 탈출 (0) | 2021.07.28 |
| [백준 9020] 골드바흐의 추측 (0) | 2021.07.25 |