이 문제에 나온 코드 그대로 적어서 내면 시간초과 나온다.
왜 그런지 알아보자.
fibonacci(10)을 호출했다고 가정해보자.
fibonacci(10) -> 1 * fibonacci(9) + 1 * fibonacci(8)
fibonacci(10) -> fibonacci(8) + fibonacci(7) + fibonacci(7) + fibonacci(6)
= 1 * fibonacci(8) + 2 * fibonacci(7) + 1 * fibonacci(6)
fibonacci(10) -> fibonacci(7) + fibonacci(6) + 2 * (fibonacci(6) + fibonacci(5)) + fibonacci(5) + fibonacci(4)
= 1 * fibonacci(7) + 3 * fibonacci(6) + 3 * fibonacci(5) + 1 * fibonacci(4)
대략 이런 식으로 계속 호출이 일어난다.
혹시, 붉은색 숫자들을 보고 떠오르는 것이 없나 ?
나는 이게 떠올랐다.

결국, fibonacci(10)을 호출하면 재귀 호출에 의해 함수들의 총 호출 횟수가 \((1 + 9 + 36 + 84 + ... + 36 + 9 + 1)\) 이 될 것이다.
일반화해보자.
\(n > 0\)일 때, fibonacci(n)을 호출하면 총 함수 호출 횟수는 \(_{n - 1}C_0 + _{n - 1}C_1 + ... + _{n - 1}C_{n - 2} + _{n - 1}C_{n - 1}\)이 된다.
또한 \(_{n - 1}C_0 + _{n - 1}C_1 + ... + _{n - 1}C_{n - 2} + _{n - 1}C_{n - 1} = 2^{n - 1}\) 임을 우린 알고 있다.
따라서, 문제에서 제공하는 소스의 시간복잡도는 \(O(2^{n})\)이다.
ㅋㅋ 지수승의 시간복잡도는.. 알고리즘 문제에서 절대 피해야하는 친구이다.
시간복잡도를 개선해보기 전에, 사실 이 문제.. 설명이 좀 틀린 부분이 있다.
호출 순서에 대한 것인데,
- fibonacci(3)은 fibonacci(2)와 fibonacci(1) (첫 번째 호출)을 호출한다.
- fibonacci(2)는 fibonacci(1) (두 번째 호출)과 fibonacci(0)을 호출한다.
이게 아니라
- fibonacci(3)은 fibonacci(2)을 호출한다.
- fibonacci(2)는 fibonacci(1) (첫번째 호출)을 호출한다.
- fibonacci(1) 이 1 출력 후, 리턴한다.
- fibonacci(2)가 fibonacci(0)을 호출한다.
- fibonacci(0)이 0 출력 후, 리턴한다.
- fibonacci(2)가 1을 출력 후, 리턴한다.
- fibonacci(3)이 fibonacci(1) (두번째 호출)을 호출한다.
- fibonacci(1) 이 1 출력 후, 리턴한다.
- fibonacci(2)가 fibonacci(0)을 호출한다.
이렇게 된다.
왜 WHY? 함수 하나가 동시에 두 개의 재귀함수를 호출할 수 없다. (멀티 쓰레드 프로그램에서는 가능.. 하지만 여기선 논외)
따라서, fibonacci(3)은 fibonacci(2)를 먼저 호출해서 모든 것을 다 처리하고 나서야 fibonacci(1)을 호출할 수 있다.
실제로 직접 코딩해서 출력해보면,
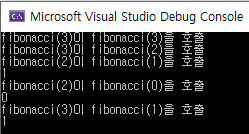
fibonacci(3)이 fibonacci(1)을 호출하는 게 가장 느린 것을 확인할 수 있다.
자, 그래서 뭐가 문제냐 ?
fibonacci(n)을 호출하면, fibonacci(n - 1)을 먼저 호출해서 모든 것을 처리한 이후에 fibonacci(n - 2)를 호출한다.
생각해보자. fibonacci(n - 1)을 처리하면서 이미 fibonacci(n - 2)가 처리됐을 것이다.
근데 한번 더 finbonacci(n - 2)를 처리하는 건 너무 비효율적이라는 생각이 든다.
이 때 필요한게, Memorization이다.
먼저, 1 출력 횟수를 구해보자.
\(n == 0\)일 때, 0
\(n == 1\)일 때, 1
\(n == 2\)일 때, 1
\(n == 3\)일 때, 2
...
이 값들을 미리 어딘가에 저장해놓자.
예를 들어 fibonacci(5)의 값은 fibonacci(5) = fibonacci(4) + fibonacci(3)이 되고,
fibonacci(4)를 구하기 위해 fibonacci(3), fibonacci(2), fibonacci(1), fibonacci(0)을 계산할 것이다.
미리 계산해놓은 것이 있다면, fibonacci(3)을 한방에 구하여 바로 fibonacci(5)의 값을 구할 수 있다.
백문이 불여일견, 피보나치 수를 구하는 코드를 Memorization을 사용하여 구현한 코드를 한번 보자.
#include <bits/stdc++.h>
using namespace std;
int fibo[41];
int fibonacci(int n) {
if (fibo[n] != -1) return fibo[n];
if (n == 0) return fibo[0] = 0;
else if (n == 1) return fibo[1] = 1;
else return fibo[n] = fibonacci(n - 1) + fibonacci(n - 2);
}
int main() {
for (int i = 0; i < 41; ++i) fibo[i] = -1;
fibonacci(40);
return 0;
}요로코롬 코딩하면 fibo의 모든 원소들이 채워질 것이다 !
혹시.. DP의 첫번째 글에서 DP에 Top-Down방식과 Bottom-Up방식이 있다라고 얘기했던 것을 기억하는가 ?
설명이 길었지만 이게 재귀를 이용한 Top-Down 방식이다.
한마디로, 40(꼭대기)에서 시작해서 밑으로 내려가기 때문에 이렇게 이름을 붙인 것 같다.
그렇다면 반대로 Bottom-Up은 ? 당연히 0부터 시작해서 위로 올라가는 것이다.
운이 좋게도 우리는 피보나치의 수의 점화식을 알고 있다.
n번째 수는 n - 1번째 수와 n - 2번째 수의 합이라는 아주 아름다운 점화식 말이다.
이걸 그대로 for문을 사용해 구현하여 40번째 피보나치 수까지 구해보자.
#include <bits/stdc++.h>
using namespace std;
int fibo[41];
int main() {
fibo[0] = 0;
fibo[1] = 1;
for(int i = 2; i < 41; ++i) fibo[i] = fibo[i - 1] + fibo[i - 2];
return 0;
}fibo행렬 채우기 끝!
Memorization이 뭔지 알았으니, 0 출력 횟수와 1 출력 횟수를 담을 배열이 두개 필요하다 ? 사실 아니다.
0 출력 횟수는 0부터 시작했을 때 나오는 피보나치 수이고,
1 출력 횟수는 1부터 시작했을 때 나오는 피보나치 수이다.
0부터 시작했을 때 : 0, 1, 1, 2, 3, 5, 8, 13, ...
1부터 시작했을 때 : 1, 1, 2, 3, 5, 8, 13, 21, ...
따라서, fibonacci(n)의
0 출력 횟수 : 0부터 시작했을 때 n번째 피보나치 수
1 출력 횟수 : 0부터 시작했을 때 (n + 1)번째 피보나치 수
가 된다.
아, 한가지 예외 케이스가 있는데 \(n == 0\)일 때는 따로 0 1을 출력하게 처리해주어야한다.
정답코드
#include <bits/stdc++.h>
using namespace std;
int fibo[41];
int fibonacci(int n) {
if (fibo[n] != -1) return fibo[n];
if (n == 0) return fibo[0] = 0;
else if (n == 1) return fibo[1] = 1;
else return fibo[n] = fibonacci(n - 1) + fibonacci(n - 2);
}
int main() {
ios::ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
for (int i = 0; i < 41; ++i) fibo[i] = -1;
int cnt;
cin >> cnt;
while (cnt--) {
int num;
cin >> num;
if (num == 0) cout << 1 << ' ' << 0 << '\n';
else cout << fibonacci(num - 1) << ' ' << fibonacci(num) << '\n';
}
return 0;
}
'BOJ_단계별로 풀어보기(9단계~) > [14단계] 동적 계획법1' 카테고리의 다른 글
| [백준 1149] RGB거리 (0) | 2022.04.07 |
|---|---|
| [백준 9461] 파도반 수열 (0) | 2022.04.06 |
| [백준 1904] 01타일 (0) | 2022.04.06 |
| [백준 9184] 신나는 함수 실행 (0) | 2022.04.05 |
| 동적 계획법(DP)에 대해서.. (0) | 2022.03.17 |